Sen(Qian)’s Memo

https://arxiv.org/abs/2312.02798

LLMの出力に自信満々に嘘を混ぜられるhallucinationは問題だ。

今までのhallucination、出力にバイアスがある系の研究は単語レベルでの検出だった。だが、最近はGPTなどからテキストシーケンスエンコーディングが一般的になっている。また、既存研究は訓練段階でhallucinationなどが起きると知られていたという仮定がある。

バイアスが事前に知らずともLLMの文章におけるバイアス検出の手法を提案する。ノードの活性化を調査することによって判断する。

この手法では、異常なsample(biasたち)をラベルせずとも学習する弱教師付きの手法を用いた。テストするときに、異常を含まない「普通」のデータがあればこの手法はできる。

事前訓練したモデルにテストデータを入れて、そこで隠れ層を調べて、どのsubsetが異常なsampleを含むかを特定する形。

生成したバイアスのものは、生成するコンテンツの分析に集中していた。coreference resolution, 感情分析, topic modeling, 予測モデルなどで下流タスクへのバイアスの伝播が調べられてきた。

しかし、これらは事前訓練した下流モデルの精度に非常による。他には主成分分析、クラスタリング、カーネル法？の識別器訓練でLLMの状態を調査している。他にも単語ペア表現間の距離メトリクスの研究をしている。

しかし、これらの研究は完全なラベル付けが前提であり、事前に定義された異常パターンのラベルが必要。

Deep Subset ScanningはCVやaudio tasksで、AEなどで異常検知に使われている。この研究はこれをさらに発展させた。

$B \in \mathcal{B}$からなる正常なデータセットと、独立したテストデータセット $\mathcal{T}$があり、それが $M$の文章を含んでいて、その中身が正常か以上かいずれも含むものである。

Encoderから入力を受けて、入力を受けて生成する中間表現を考える。

$M$個のテスト文章があり、それぞれの層 $l$でのベクター表現は $[Z_1^l, \cdots, Z_M^l]$であるとする。各文章の持つアクティベーション(ベクター表現)は $Z_i^l$であるが、このベクトルの成分はそれぞれ $J$個のニューロンに対応し、 $O_1^l, \cdots, O_J^l$である。

ここで、 $Z^S \subseteq Z, O^S \subseteq O$だとする。これの直積 $S = Z^S \times O^S$を考える。

ある評価関数 $F(S)$を用いることで、これが最大値を取るような $S$を見つける=最も異常が多いような $S$を見つけたい。

一般的には $F$は事前に決めた概形を持つ関数を使う。

例えば、ガウス分布やポアソン分布を使う時はデータがそれに従うと仮定し、平均と分散を求めて、そこで分散が一定以上などの条件を満たすものを異常として扱い、それをもとに $S$を決める感じ。

しかしこの論文では、ノンパラメトリックな方法を使う=Non-Parametric Scan Statisticsを使う。なぜなら特定のlayerで分布を使って仮定すると全く当てはまらないぐらい、ズレている可能性があるから。以下のように解く。

1. 様々なアクティベーション $Z_i^l$を考える。
2. 全てのアクティベーションを見て、各次元(複数のアクティベーションベクトルの指定の次元)におけるActivationの分布の違いやシフトを定量化する。
   1. ここで各次元についてのp値を計算する。
      1. パラメトリックな方法ならば、平均や分散がわかるので、累計度数分布を見ればいい。
      2. しかし今回はノンパラメトリック。ランダム化テストやブートストラップなどを使う。
         ランダム化テスト

         1. 2つのグループのデータを準備する。
         2. 観測された効果(平均値の差など)を計算。
         3. データをランダムにシャッフルし、2つのグループをかき混ぜる。
         4. 元のものと比較する。この時、観測された効果が極端に小さくor大きくなった割合を計算する。この割合をp値とする。(あまり変わらない=2つのグループ内でだいたい同じ)
         ブートストラップ

         1. 元のデータセットからサンプリングして、新たなセットを作る。
         2. これについて関心がある統計量(平均、中央値、分散など)を計算する。
         3. これを多数繰り返すことで、各統計量についての離散分布が得られる。
         4. その離散分布を元に、p値を計算する。(だってこれガウス分布でしょ？ここではパラメトリックにやってOK)
   2. これを基準分布と比較する中で、どのノードが異常なアクティベーションをしてるかを識別できる。
   3. たとえば、明らかに基準分布の中央値よりはるかに大きいなどなら、異常だとみなす。それを見るために、p値を計算する。(異様に小さい場合は異常)

正常なデータセット $B$の入力のアクティベーションを $z_{ij}^{Bl}$( $l$層目、データが $B$、 $j$個目の $B$のサンプル文章がアクティベーションを示すベクトル　これの $i$次元目の成分)とする。テストデータセット $T$のアクティベーションを $z_{ij}^{Tl}$と表せる。

各ニューロン ($J$次元あるもの)について、 $B$も $T$もそれぞれソートする。正直以下の式さえ求めればいいので、ソートはしなくてもよい気はするけどね。

以下の式で $T$に属する $j$番目の文章の $l$層目のアクティベーションのベクトルの$m$次元目について、p-valueは以下のように推計できる。

つまり、 ある入力 $t \in T$について、指定の層の指定のニューロンの値について、$B$のものと比べてどれほど超えてしまっているかが得られる。これが異様に小さいor大きいと、異常だという認定。

p値が一様分布からどれだけずれているかを示すのに、何かしらの指標が必要である。各種の指標 $\alpha$のなかで、最も差異が出た指標を使う。以下のような形。

　$N(S)$は部分集合 $S$においての経験的p値、 $$\alpha

• $N(S)$は部分集合 $S$に含まれている経験的p値の数(なんだこれ)
• $\alpha$は有意水準
• $N_{\alpha}(S)$は部分集合 $S$に含まれている経験的p値の数のうち、有意水準を下回る数。
• $\phi$は何かしらの統計量　後述のHigher Criticism Test Statistic

有意水準(左端と右端の和)は0.05から0.5まで、0.05刻みで全部試した。

High Criticism Test Statisticという統計量をこの論文では使う。

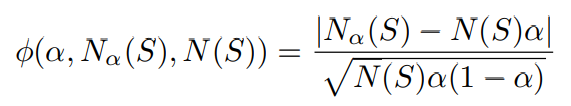
テストデータ内の以上データが少ない場合では、特に $S$は小さい集合が望ましいらしい。

Fast Generalized Subset Scanningという手法を使う。これは計算量を $O(2^E)$から $O(E)$まで、指定のデータ量を用いて、局所最適をある程度許容しながら探索している。

異常に小さいp値の集合 $Z_{SL}$と以上に大きいp値の集合 $Z_{SR}$を集めて、 $Z_{SL} \cup Z_{SR}$にする。

もう1つのやり方として、 $k$回イテレーションして毎回もっとも異常だったものを取り除いてもう1回イテレーションみたいな感じ。ようわからん。

BERTはこの手法は効果はあまりなかった。内部状態でHallucinationを表現はなかなかできない。

だが、GPTに匹敵するモデルのOPTはちゃんと内部状態でHallucinationを起こしていたかも。

確かに既存手法に匹敵するが、既存手法がそもそもよくない。

統計的指標でcos類似度を見るやつもあったらしい。

感覚: 見る層は後ろの本質情報の方がよくね？とは思った。そもそもみんな性能良くないな…